すうがくパパ
こんにちは、すうがくパパです。
今回は入試でもよく出る「平方根(へいほうこん)」の特徴を見ていきましょう。√(ルート)の計算やグラフの動き方がテーマです。
√(ルート)ってどんな数?
「平方根」とは、二乗(×2)すると、「ルート」の中に書かれた数字になる数のことです。
たとえば、
\(\sqrt4\)=2
\(\sqrt9\)=3
のように、ピッタリ整数になる場合もあります。
でも、そういう例は実は少数派。たいていは次のようになります
\(\sqrt2\) =1.41421356…
\(\sqrt3\) =1.7320508…
このように、小数点以下がずーっと終わらず、しかも規則性もないのが平方根の特徴です。
平方根のグラフはどんな形?
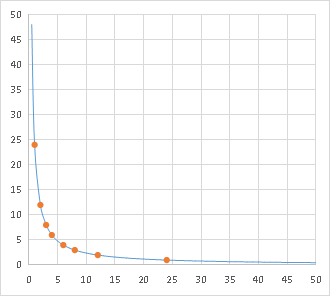
平方根の関数は、
\(y=\sqrt x\)という形をしています。両辺を二乗すると
\(y^2=x\)ですから、二次関数(放物線)を横に寝せた形になることが分かります。
xが大きくなっても、yの増え方はだんだんゆるやかになるのが特徴です。
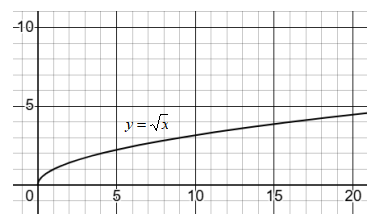
グラフを動かして比べてみよう
ところで、
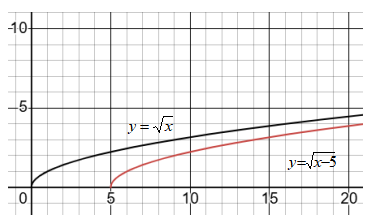
もとのグラフ(黒線):\(y=\sqrt x\)
を右に5ずらしたグラフ(赤線):\(y=\sqrt{x-5}\)
この2つのグラフの差を調べると、面白い発見があります。
たとえば、x = 9 のとき:
黒線:\(y=\sqrt9=3\)
赤線:\(y=\sqrt{9-5}=2\)
となり、yの値がちょうど1離れているのが分かります。
でも、xがもっと大きくなるとどうなるでしょう?
x = 16 のとき:\(\sqrt16-\sqrt{16-5}≒4−3.316≒0.684\)
x = 25 のとき:\(\sqrt25-\sqrt{25-5}≒5−4.472≒0.528\)
というふうに、差は1よりどんどん小さくなっていくんです。
平方根の問題は、よく「両辺を二乗して」解く場合が多いですが、
グラフの特徴や数の性質も知っておくと、さらに理解が深まります!
それではまた!