すうがくパパ
平行線は、 関数 や 図形 の入試問題でよく出ます。そして、補助線としてサッと引くだけで一気に解けることも。ここでは覚えておきたい 3 つの特徴を整理します。
まずは “平行線” のキホンをおさえよう
平行線の一つ目の特徴は、同位角とか、錯角の位置にある角度が等しくなるという点です。
たとえば、下の図では、●をつけた角度がすべて等しくなっています。
こういった特徴は、特に図形の問題で相似な(もしくは合同な)三角形を探すのに役立ちます。
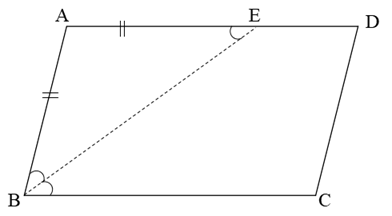
また、下の図のように平行四辺形ABCDの角Bに角の二等分線を引いてみると、
三角形ABEが二等辺三角形になりますね。
これは、∠EBCと∠BEAが錯角になっているからで、図形の問題でよく見かけますよね。
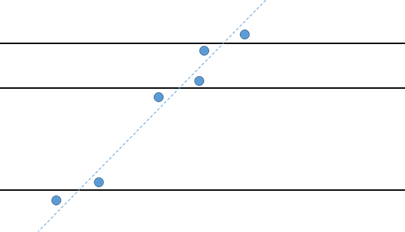
次に、二つ目の特徴は、平行な線で区切られた線分がすべて同じ比率になるという点です。
下の図でいうと、青・黄・赤いずれの点線も線分の長さの比(a:b)が等しくなります。
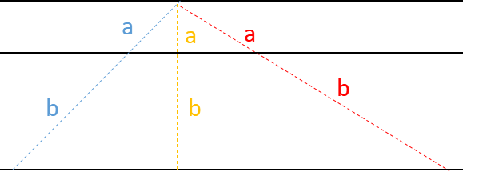
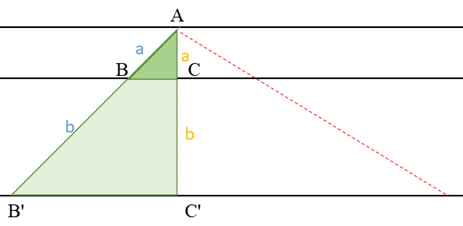
なぜなら、下の図の三角形ABCと三角形AB’C’のように相似の三角形を作ることができ、
その相似比(△ABC:△AB’C’= a : a+b)から導かれるからです。
ちなみに、この場合BC:B’C’もa : a+bになりますね。
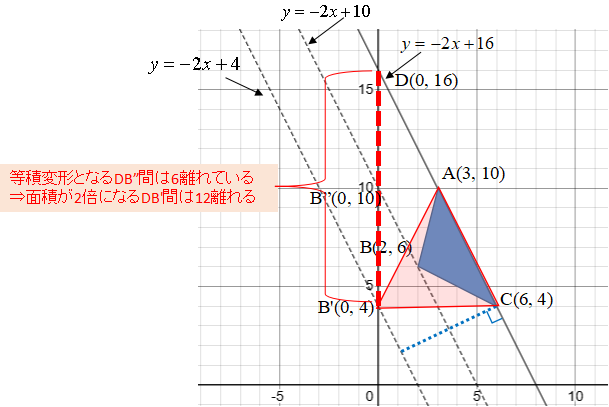
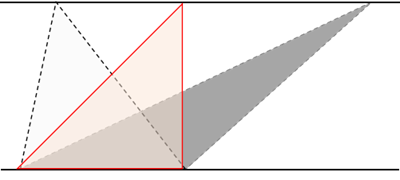
最後に、三つ目の特徴は、底辺が同じで,もう 1 点が底辺と平行な直線上にある三角形の面積は ぜんぶ同じ、という点です。
高さが同じになるからで、いわゆる等積変形と呼ばれています。「ちょっとずらしても面積キープ」というテクは面積の問題でとても役に立ちますよね。
ちなみに、これらの特徴を組み合わせることで、実戦での活用の幅がグッと拡がります。
話が長くなるので、続きはこちらで!