数学の問題を解くときの「着想」ってナニ？（その1）

このブログでは、「数学の問題をどうやって思いついて解くか＝着想力を伸ばすこと」をテーマにしています。私自身、ムスコの高校受験を手伝っていたときに感じたのは、「答えの出し方」よりも、「どうやってその答えの出し方に気づくか」が大事だということです。

「着想」って何をすること？

それにしても、「着想」っていったい何をすることなのでしょう？言いかえれば、何をすればその“解き方”にたどり着けるのでしょうか？

ここがわかっていないと、「こういうときはこう解く」という解き方のパターンを覚えるだけの勉強になってしまいます。それも一つの方法ですが、入試でよく出る“ひねった問題”には対応しづらくなります。

でも正直に言うと、私自身が「着想ってこういうことなんだ！」と本当に分かったのは、ムスコの受験が終盤にさしかかった1月のことでした。今回はそのときムスコに話した内容を紹介します。

ゴールの見えない山道を歩くように

難しい問題になると、最初から「これだ！」という解き方が見つかることは少なくなってきます。

イメージとしては、山に囲まれてゴールの場所が見えないところからスタートしているような感じです。

しかも、何も考えずに進みはじめると、間違った方向に行ってしまい、いつまでたってもゴールに近づけません。

「特徴」を見つけて考えを進める

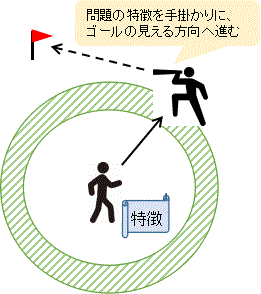
でも、どんな問題にも、必ず「ヒント」となる“特徴”があります。

たとえば、数式の問題なら、うまく因数分解できそうだったり、図形の問題なら、直角三角形が相似になっていそうだったり、そんなポイントです。

その“特徴”に気づいて、「じゃあ、ここから何が言えるかな？」「さらに何がわかるかな？」と考えを進めていくこと――これが「着想」なのです。

一気に答えにたどりつけなくても、少しずつ正しい方向に進めていれば、やがてゴールまでの道すじが見えてきます。

模範解答の見方にも注意！

それでは、「特徴」からどうやって次のヒントを見つけていけばいいのか？

この続きを話すと長くなるので、別の記事でまた紹介したいと思います。

ちなみに、問題集や模試の模範解答は、「こうやって一直線にゴールできますよ」という最短ルートを示したものです。

もちろん、それを読むのも大事です。でも、「どうしてその解き方にたどり着けたのか？」という理由を、自分の中でちゃんと理解することが、本当に力になると思います。