すうがくパパ
こんにちは、すうがくパパです。
今回はちょっと地味だけど、入試で差がつく「反比例」と「整数」の関係について見ていきましょう。
一次関数や二次関数ばかりじゃない!
中学校では、
・一次関数:\( y=3x+7 \)
・二次関数:\( y=\displaystyle \frac {1}{2}x^2\)
といった関数が中心になりますよね。
でも実は、
\(y= \displaystyle \frac{24}{x} \)
もしくは
\( xy=24 \)
のような「反比例」も、入試にときどき出てくるんです。
ただ、演習問題ではあまり扱わないことが多く、苦手意識を持っている人もいるかもしれません。
グラフで見てみよう!
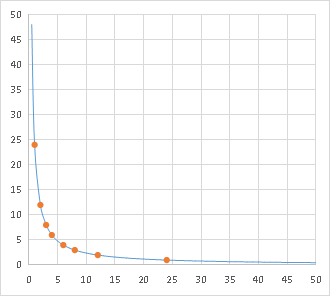
それでは、たとえば
\(y= \displaystyle \frac{24}{x} \)(x>0, y>0の範囲だけ表示)
のグラフを見てみましょう。
このグラフは、どこまで軸を伸ばしても x軸やy軸と交わることはありません。
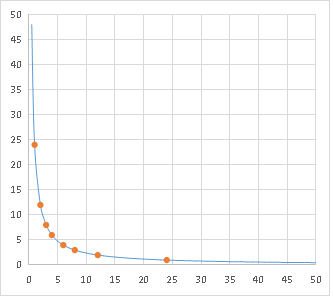
また、xもyも整数になる点は、グラフ上にいくつかしかありません。
よく見てみると、それらの x座標やy座標は「24の約数」 になっているんです。これは、グラフの式を
\( xy=24 \)に変形できることから分かりますね!
このように、反比例の式は整数が絡む問題のヒントになる場合が少なくありません。
入試で出てくる応用問題では?
反比例の式がそのまま入試に出ることはあまりありません。
でも、ちょっと式を変形すると反比例になることがあります。
たとえば、こんな式があったとします。
\(xy-5x-3y-9=0\)これは、
\((x-3)(y-5)=24\)(※)
に変形できるワケですが(※のような変形を個人的には「因数分解くずれ」と呼んでいます)、
\(X=x-3\) 、\(Y=y-5\)と置けば、
\(XY=24\)
という形になり、反比例の問題に早変わり!
反比例のポイント!
反比例の式が出てきたら、「積が一定になる整数の組み合わせ」を探すという視点を持ちましょう。
また、式変形で反比例の形に持ち込めないかを考えるのも大切です。
ちょっとした工夫で、問題の見え方が大きく変わることもあります!