すうがくパパ
前回のコラムでは、おさえておきたいキホンとして、平行線の3つの特徴を紹介しました。
今回はそれらの特徴を活用して、入試に出るようなむずかしめの問題にチャレンジしてみましょう。
Contents
まずはキホンのおさらいから!
平行線の3つの特徴はこちらですね!くわしい説明はこちらをご覧ください。
同位角とか、錯角の位置にある角度が等しくなる
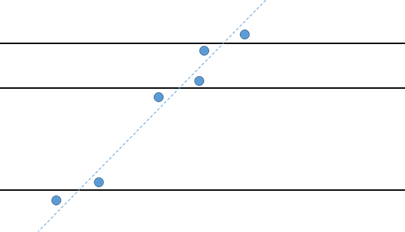
平行な線で区切られた線分がすべて同じ比率になる
底辺が同じで,もう 1 点が底辺と平行な直線上にある三角形の面積は ぜんぶ同じ
ハイレベルの問題にチャレンジ!
さて、これらの平行線の特徴を組み合わせることで、実戦での活用の幅がグッとひろがります。
さっそくこちらの問題にチャレンジしてみましょう!
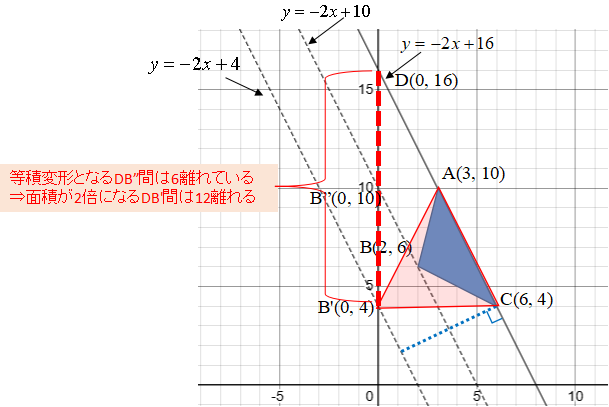
以下の図のようにA(3, 10)、B(2, 6)、C(6, 4)からなる△ABCがある。
辺CAを共通としつつ、もう一つの点がy軸上にあって面積が△ABCの2倍となるような点B’を求めなさい。
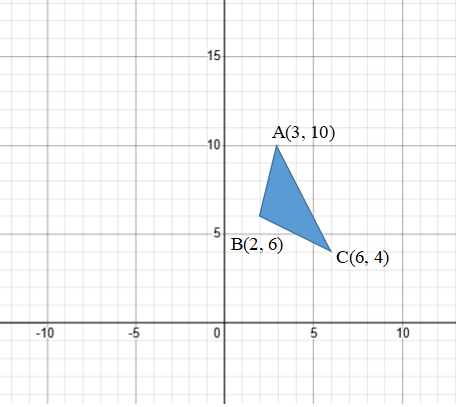
パッと見た感じでは、とても難しそうですね。。
いきなり面積2倍の三角形を探すのはシンドイので、まず同じ面積となる点B”から探すことにしましょう。
辺CAは直線\(y=-2x+16\)上にありますから、これと同じ傾きで、点Bを通る直線\(y=-2x+10\)上に点B”をとると、等積変形の三角形を作ることができます。(三つ目の特徴を使った形になりますね。)
ちなみに点B”がy軸上にある場合は、B”(0, 10)となります。
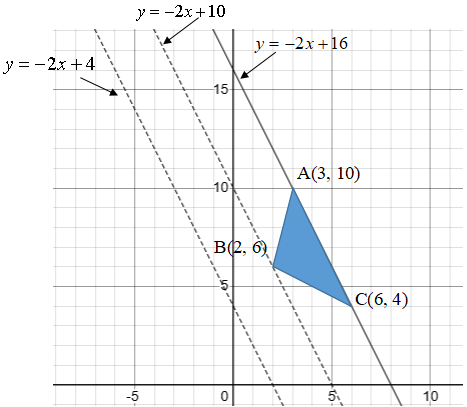
次に面積が2倍になる場合を考えてみますが、ここで二つ目の特徴を思い出しましょう。
本来は底辺CAに対する高さ(下図の青点線)が2倍になるよう考えたいのですが、計算がヤヤコシイので、
代わりにy軸の線(下図の赤点線)で考えてみることにします。
まず、直線CA(\(y=-2x+16\))とy軸との交点(つまりy切片)をD(0, 16)とすると、
△ABCと面積が等しい場合のy軸上の点B”(0, 10)との間の距離(DB”間の距離)は
16-10=6離れていることが分かります。
したがって、面積が2倍になるy軸上の点B’は点Dから6×2=12離れていることになり、
点B’は(0, 4)となります。
ちなみに辺CAと平行で点B’を通る直線\(y=-2x+4\)上に点を取ると、
すべて△ABCの2倍の面積の三角形を作ることができます。
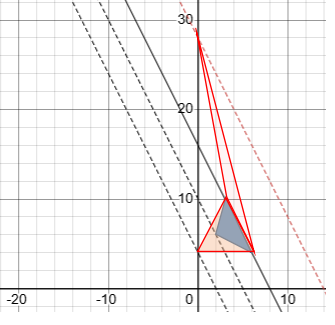
ところで、点B’は直線\(y=-2x+16\)の右側にもう一点あります。
点Dと点B’は12離れているので、逆方向に12離れている(0, 28)も該当するのです。
つまり、直線\(y=-2x+28\)上に点をとっても、△ABCの2倍の面積の三角形を作ることができるのです。
あまりキレイに描けていませんが、△ABCを青色、面積が2倍になり点B’がy軸上にある二つの△AB’Cを赤色で示しておきます。
いかがでしたでしょうか?
平行の特徴はシンプルですが、使いこなせると難しく見える問題もスムーズに解けますよ!