九九の総和って、いくつになる？

小学校で習う九九（1×1、1×2、・・・・、9×9）をすべて足し合わせると、いくつになるのでしょうか？フツーに考えると、結構難しいですよね。

まずは基本から

これを考える前に、基礎問題として

1から9までの整数の総和（1+2+3+4+5+6+7+8+9）がいくつになるか、考えてみることにしましょう。

ここで、1+2+・・+9と、この順序をひっくり返した9+8+・・+1を足し合わせると、

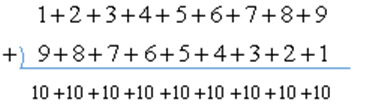
となり、10を9つ足し合わせて90になると分かります。ですから、1+2+3+4+5+6+7+8+9は、その半分の45になります。

一の段、二の段を足してみるとどうなるか

さて、本題の九九です。まず、一の段の総和を考えてみると

(1×1)+(1×2)+・・・+(1×9)=1×(1+2+・・・+9)　　（①）

になりますね。

同じく二の段の総和は、

(2×1)+(2×2)+・・・+(2×9)=2×(1+2+・・・+9)　　（②）

になります。同じく、九の段の総和は、

(9×1)+(9×2)+・・・+(9×9)=9×(1+2+・・・+9)　　（③）

となりますね。

ここで①~③の右辺に注目すると、九九の総和は

1×(1+2+・・・+9) + 2×(1+2+・・・+9) + ・・・+9×(1+2+・・・+9)

=(1+2+・・・+9)×(1+2+・・・+9)　　（④）

になります。

さて、冒頭で説明したように、1+2+・・+9=45ですから、④より九九の総和は

45×45 = 2025となります。

九九の総和の計算方法は他にも色々あるようですが、私が考えた方法は以上になります。

受験生のみなさんへ

「九九」はあまりにも当たり前すぎて、あらためて考えることは少ないかもしれません。でも、

というふうに、よく見ると面白い法則や構造が隠れています。

こうした「身近な数のしくみ」に気づけると、数学のセンスがどんどん磨かれていきます。
受験にも、将来にも役立つ“着想のタネ”を育てていきましょう！