私たちは普段、0, 1, 2, 3, 4, 5, 6, 7, 8, 9という10種類の文字を使いながら、当たり前のように数字を書いたり計算したりしています。詳しい話は後ほどキチンとしますが、私たちは「10進法」の世界で生活しています。
しかし、コンピューターの世界では「2進法」、つまり0と1だけを使って様々なデータを表現していると聞いたことがある人もいるでしょう。
「2進法」があるわけですから、「3進法」や「5進法」、「12進法」とかも当然あるワケですが、そもそも「n進法」とはいったい何なのでしょうか？私自身は、自分が中学生の頃を思い出すと、「n進法」が正直とっつきにくくて苦手だった記憶があります。
ちゃんと理解できるようになったのは多分オトナになってからです。この間ムスコに説明したところ、イッパツで理解してもらえたので、これから紹介したいと思います。
例えば、コインでも団子でも良いのですが、たくさんのモノを数えるときに、一列に並べてひたすら数えるのはシンドイですよね？下の図ぐらいだったら何とかなりますが、例えばこの10倍とか100倍になったりすると、気が遠くなるわけです。
そこで、ある程度数えたところで一つの箱にまとめたり、束ねたりすることで、数えやすくなるわけです。
ここで団子やコインを何個でまとめるかが問題になりますが、10個でまとめるのが「10進法」の考え方になります。ちなみに、箱の数がだんだん増えていくと、さらに大きな箱で10個の箱をまとめます。この大きな箱には、10個入りの箱が10個入っているので、団子もしくはコインが10×10=102=100個入っていることになりますね。
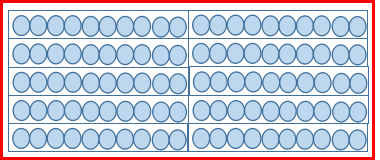
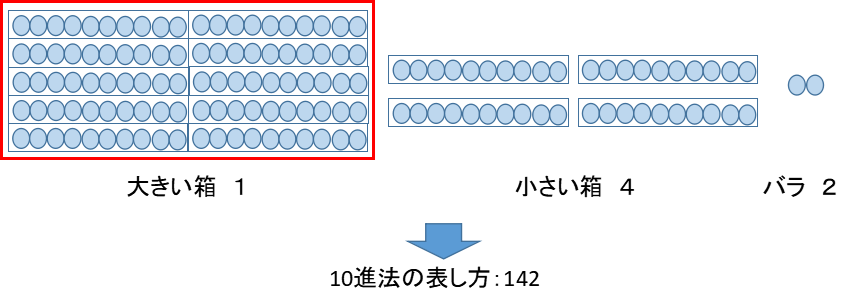
ということは、例えば142個の団子があるときは、大きな箱1つと小さな箱4つ、そしてバラの団子・コイン2つに分けて数えるということなります。つまり、
\(142=1\times10^2+4\times10+2\)ということですね。
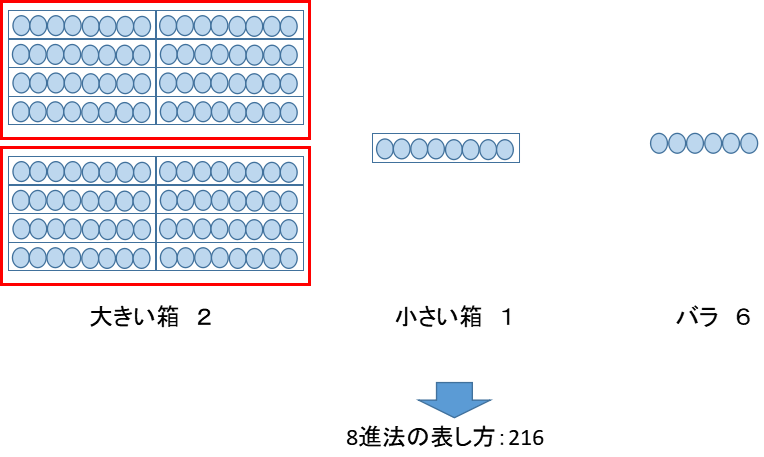
それでは、8進法だとどうなると思いますか？8進法では8個で一つの箱にまとめていくことになります。
このケースでは、大きい箱が2つ、小さい箱が1つ、バラ6に分けられます。つまり、
\(142=2\times8^2+1\times8+6\)となり、8進数では216と表されることになります。
それでは、12進法の場合はどうでしょうか。12進法では12個で1つの箱にまとめていくことになります。
この場合、大きな箱はゼロ、小さな箱は11個、バラ10個になります。つまり、
\(142=0\times12^2+11\times12+10\)となります。
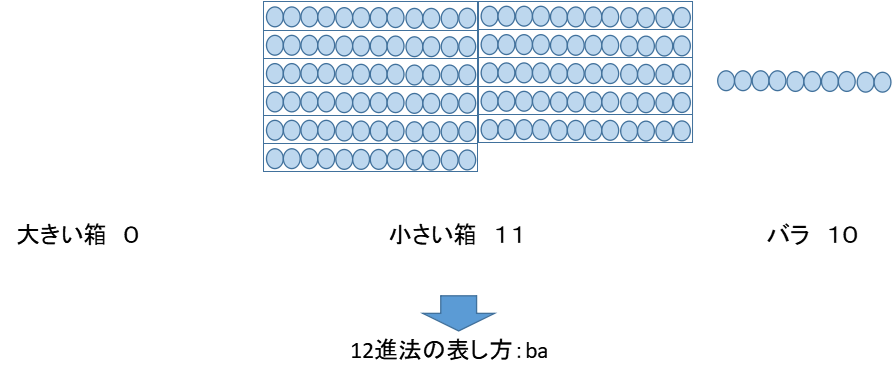
ところで、12進法では数字を表す文字が0から9では足りません。そこで、9の次の数字をa、その次の数字をbとします。（その次は12進法では10になります。）
この場合、142を12進法で表すと、「ba」と書かれることになります。
いかがでしたでしょうか？個人的には「n進法」が分かりにくいのは、「進」という文字に原因があると思っています。モノを数えるときの箱の大きさをイメージすることで、「n進法」を身近に感じられるのではないでしょうか。ちなみに、鉛筆の箱は12本入りで1ダースと呼ばれますが、これは一種の12進法ですね。
