すうがくパパ
こんにちは、すうがくパパです。
学校で「素因数分解」を習ったとき、「いくつか数字を分解して終わり。これって何に使うの?」と思ったことはありませんか?
でも実はとっても役立つんです!
Contents
最大公約数・最小公倍数に大活躍!
最大公約数や最小公倍数の問題を考えるとき、素因数分解は大変便利です。
例えば「60と96の最大公約数」を求めたいとき。
それぞれ素因数分解すると、
\(60=2^2\times3\times5\)
\(96=2^5\times3\)
となります。
このとき「両方に共通する因数」をできるだけたくさん集めたものが、最大公約数になります。
つまり、 \( 2^2\times3=12\) が答え!
逆に、最小公倍数を求めるときは、「どちらかに出てくる素因数のうち、指数が大きい方」を全部集めて、
\(2^5\times3\times5=480\)と求められます。素因数分解を使うと、こうした計算があっという間にできちゃいます!
約数の個数もわかる!
次に、「60の約数は何個ある?」という問題を考えてみましょう。
まずは素因数分解
\(60=2^2\times3\times5\)
なので、60の約数は、2, 3, 5をいくつ含むかに応じて、必ず以下の式で表すことができます。(ここで、含まない場合を「ゼロ乗(=1)」として扱うのがミソです。)
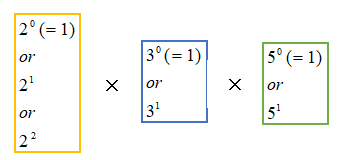
ここで、2の「含み方」は3通り、3の「含み方」は2通り、5の「含み方」は2通りありますので、約数の数は、これらの組み合わせの数となり、3×2×2=12通りとなるのです。
小さい数なら数えてもいいけれど、大きな数になると素因数分解がないととても大変。
ぜひこのやり方をマスターしておきましょう!