「実践!着想トレーニング」のコーナーでは、高校入試レベルの問題を取り上げ、問題を解くための「きっかけ」をつかむ練習をしたいと思います。
今回はこちらの問題を考えてみましょう!
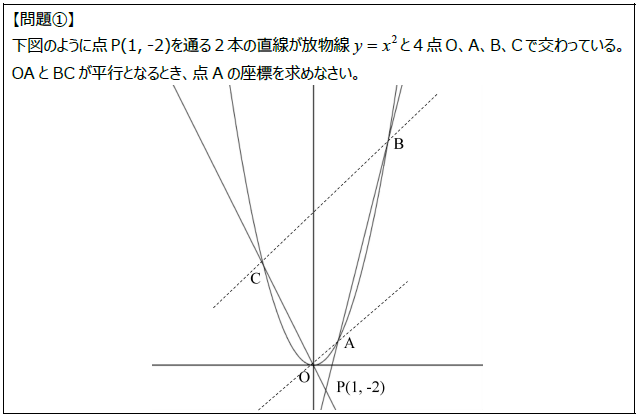
下図のように点P(1, -2)を通る2本の直線が放物線\(y=x^2\)と4点O、A、B、Cで交わっている。
OAとBCが平行となるとき、点Aの座標を求めなさい。
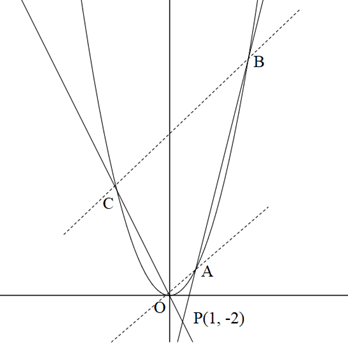
点P(1, -2)と放物線\(y=x^2\)ぐらいしか数字が与えられていないので、なかなか手がかりがありませんね。。。
「OAとBCが平行になる」という特徴をどう使うかがポイントになりそうです。
でも、具体的にどう考えればいいんでしょうかね?
詳しい解説と解答を以下の「着想ノート」にまとめました。特に「着想のポイント」のコーナーは必見です!
どうぞ、ダウンロードしてください。(もちろん無料です)
このほか、いろいろな問題をnoteに「着想ノート」としてアップしました。
関数編は【問題①】~【問題⑧】まであります。色々な図形と組み合わせた問題が多いですね。
最初に紹介した【問題①】以外は有料ですが、「着想のポイント」のコーナーを読めば、
問題を解くための「目のつけどころ」が分かり、短期間で着想力がアップ!
いずれも入試によく出そうな、即効性のある問題をそろえました。ぜひチャレンジしてください!
【問題①】~【問題⑧】の「着想ノート」をまとめてダウンロードしたい方はこちらから、
気になる問題だけダウンロードしたい方は、それぞれ以下にリンクを貼っておきましたので、そちらからどうぞ!
ちなみに、それぞれの問題をご紹介しますね。【問題①】の「着想ノート」は上からダウンロードできますよ。
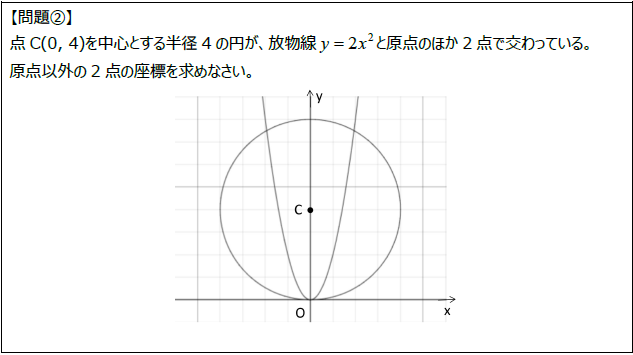
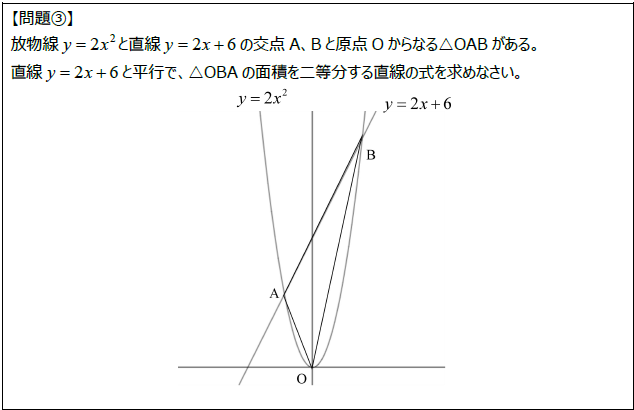
【問題②】【問題③】の「着想ノート」は2題まとめてこちらからどうぞ。
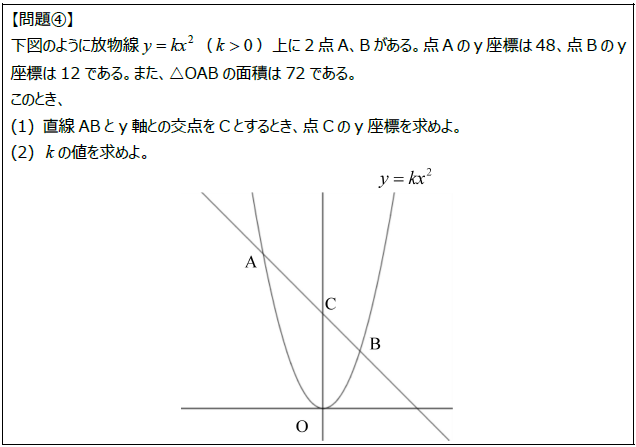
【問題④】の「着想ノート」はこちらからどうぞ。
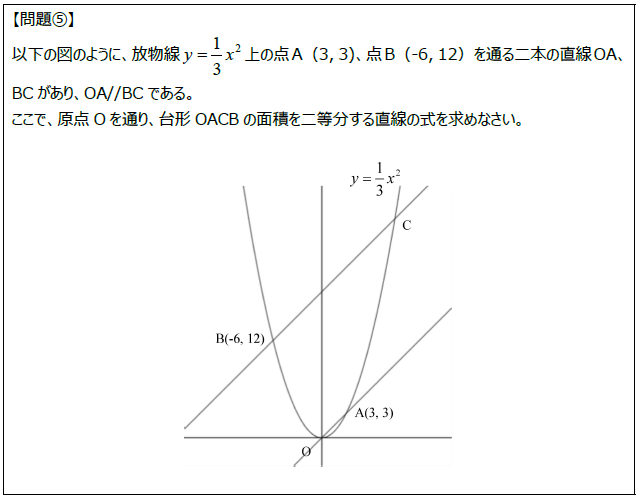
【問題⑤】の「着想ノート」はこちらからどうぞ。
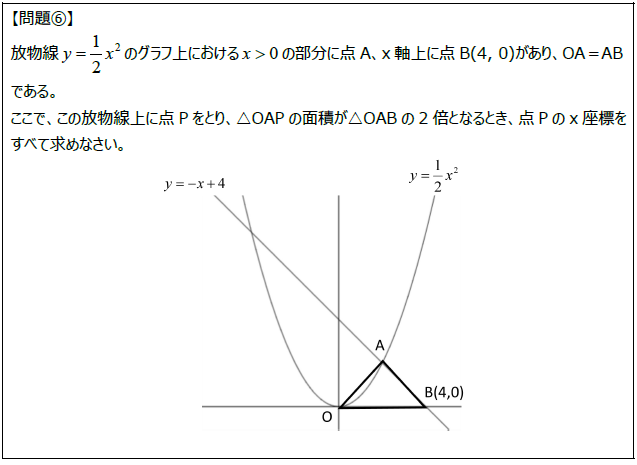
【問題⑥】の「着想ノート」はこちらからどうぞ。
【問題⑦】の「着想ノート」はこちらからどうぞ。

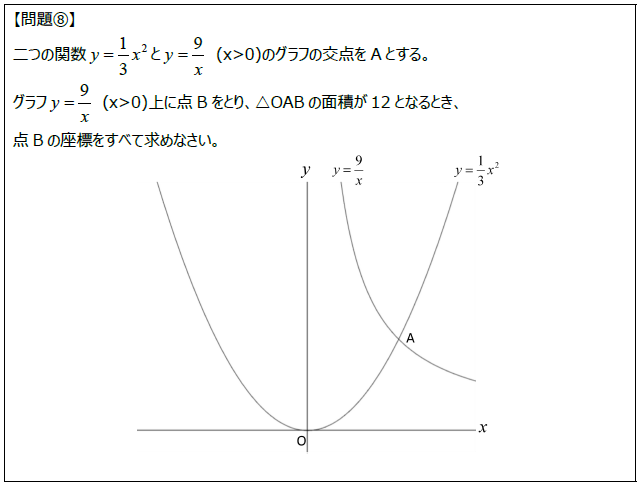
【問題⑧】の「着想ノート」はこちらからどうぞ。
最初に紹介した【問題①】以外は有料になってしまいますが、
「着想のポイント」のコーナーを読めば、
問題を解くための「目のつけどころ」が分かり、短期間で着想力がアップ!
また、【問題①】~【問題⑧】の「着想ノート」をこちらからまとめてダウンロードすると、割引価格で少しオトクです!
「着想ノート」をぜひ見にきてください!